1. Movimiento de un Proyectil
El movimiento de un proyectil es un ejemplo clásico
del movimiento en dos dimensiones
con aceleración constante. Un proyectil es
cualquier cuerpo que se lanza o proyecta por medio
de alguna fuerza y continúa
en movimiento por inercia propia. Un proyectil es un objeto sobre
el cual la
única fuerza que actúa es la aceleración de la gravedad. La gravedad actúa para
influenciar el movimiento vertical del proyectil. El movimiento horizontal del
proyectil es el
resultado de la tendencia de cualquier objeto a permanecer en
movimiento a velocidad
constante.
2.
Análisis del
movimiento de Proyectiles
Se examina sólo trayectorias suficientemente cortas para que la fuerza
gravitacional se pueda
considerar constante en magnitud y dirección. También
hay que analizar no tener en cuenta los
efectos de la resistencia del aire;
Estas hipótesis simplificadas constituyen la base de un
modelo idealizado del
problema físico. Como, en este caso idealizado, la única fuerza que
actúa sobre
el proyectil es su peso considerado constante en magnitud y dirección, es mejor
referir el movimiento a un sistema de ejes coordenadas rectangulares. Se toma
el eje x
horizontal y el eje y verticalmente hacia arriba.
3.
Tiro Parabólico
Un tiro parabólico en el cuerpo se lanza con un ángulo de elevación. Es resultado de la
combinación de dos movimientos
independientes el primero es un
movimiento
uniformemente acelerado (mrua) que se expresa en forma de tiro
vertical durante el ascenso y
como caída libre desde el momento que empieza a
descender.
4.
Representación
gráfica del Tiro Parabólico
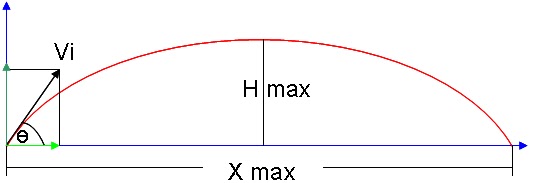
En la figura se muestra un esquema de una trayectoria parabólica. Se
observa que la
velocidad inicial, como todo vector, se separa en sus
componentes rectangulares: la
componente horizontal, Vx y la componente
vertical Vy.
Durante el ascenso, la componente vertical de vector velocidad Vy,
disminuye conforme se
eleva, por lo que su magnitud es cada vez más pequeña: se
hace cero un momento en el
punto más alto y de nuevo empieza a crecer a medida
que el cuerpo cae.
Por su parte la velocidad horizontal Vx, permanece constante, por lo que su
magnitud no se
altera. En la trayectoria analizada solo se muestran los puntos
de mayor interés para describir
este movimiento. Dichos puntos son:
• Angulo de disparo: Es la
inclinación con la que sale impulsado el proyectil. Se mide respecto al plano
horizontal como se muestra en la figura:
•Velocidad inicial: Es la
velocidad con la que el proyectil emprende el movimiento de tiro parabólico y
que es suministrada por un agente externo como se muestra en la figura:
5.
Tiro Horizontal
El tiro horizontal se diferencia del tiro parabólico en que al inicio del
movimiento el proyectil
sólo presenta una velocidad horizontal, (Vx), debido a
que no existe ángulo de inclinación. Por
tanto no presenta velocidad vertical
inicial, (Viy=0), lo que implica que Vx= Vix. Su gráfica
característica se
muestra en la figura.
Al analizar el tiempo de caída de dos cajas lanzadas al mismo tiempo desde
un avión que
vuela horizontalmente y con velocidad constante, ambas llegan al
suelo al mismo tiempo,
aunque la caja 1 se dejó caer libremente, mientras que
la caja 2 se lanzó hacia la derecha con
cierta velocidad horizontal, probándose
con ello la independencia de los movimientos
correspondientes, como se
muestra en la figura.
6.
Lanzamiento
Inclinado
Consiste en estudiar el caso de una partícula o proyectil que se lanza con
una velocidad
inicial, formando un ángulo q0 con la dirección
horizontal. Su velocidad cambia
constantemente debido a la acción del campo
gravitatorio. Los componentes rectangulares de
la velocidad inicial y. (Los
subíndices se utilizan para indicar los valores iníciales de en cada
uno de los
ejes). Si no existiera la atracción gravitatoria, en tiempos t1, t2,
t3, … ocuparía
respectivamente posiciones tales como A, B, C, D, y
el movimiento sería rectilíneo uniforme
de velocidad constante , Sin embargo
como el proyectil está sometido a la fuerza de atracción
gravitatoria, a la vez
que se mueve según la recta AE, cae verticalmente, y al final de los
tiempos
indicados las posiciones del proyectil son respectivamente A', B',C,'D' … La
curva
que une estos puntos determina la trayectoria del proyectil, que corresponde
a una parábola .
No hay comentarios:
Publicar un comentario